〇正弦波のラ(440Hz)の音
import numpy as np
import matplotlib.pyplot as plt
import wave
import struct
filename = "sine_440Hz.wav"
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)
s = a * np.sin(2.0 * np.pi * f0 * n / fs)
plt.plot(s[:int(fs/f0)])
plt.show()
s = [int(x * 32767.0) for x in s]
bin = struct.pack('h' * len(s), *s)
w = wave.Wave_write(filename)
p = (1, 2, fs, len(bin), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(bin)
w.close()
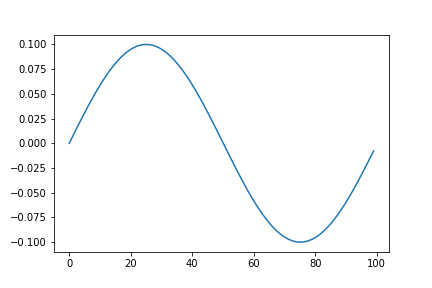
sine_440Hz.wav
〇矩形波のラ(440Hz)の音
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import wave
import struct
filename = "square_440Hz.wav"
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)
s = a * signal.square(2.0 * np.pi * f0 * n / fs)
plt.plot(s[:int(fs/f0)])
plt.show()
s = [int(x * 32767.0) for x in s]
bin = struct.pack('h' * len(s), *s)
w = wave.Wave_write(filename)
p = (1, 2, fs, len(bin), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(bin)
w.close()
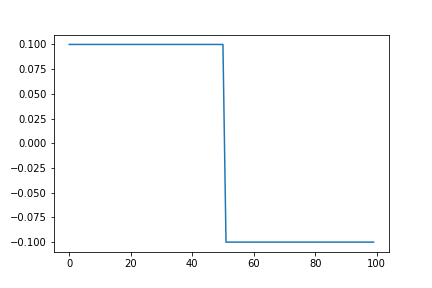
square_440Hz.wav
〇三角波のラ(440Hz)の音
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import wave
import struct
filename = "triangle_440Hz.wav"
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs + np.pi/2, 0.5)
plt.plot(s[:int(fs/f0)])
plt.show()
s = [int(x * 32767.0) for x in s]
bin = struct.pack('h' * len(s), *s)
w = wave.Wave_write(filename)
p = (1, 2, fs, len(bin), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(bin)
w.close()
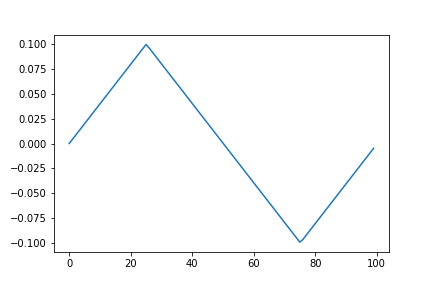
triangle_440Hz.wav
〇のこぎり波のラ(440Hz)の音
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
import wave
import struct
filename = "sawtooth_440Hz.wav"
a = 0.1
f0 = 440
fs = 44100
sec = 3
n = np.arange(fs * sec)
s = a * signal.sawtooth(2.0 * np.pi * f0 * n / fs)
plt.plot(s[:int(fs/f0)])
plt.show()
s = [int(x * 32767.0) for x in s]
bin = struct.pack('h' * len(s), *s)
w = wave.Wave_write(filename)
p = (1, 2, fs, len(bin), 'NONE', 'not compressed')
w.setparams(p)
w.writeframes(bin)
w.close()
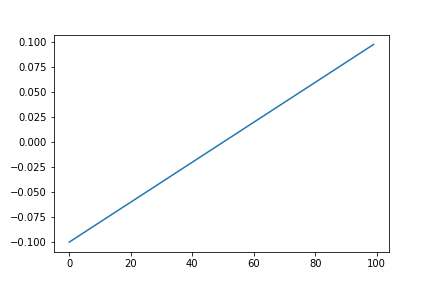
sawtooth_440Hz.wav

